2022年-行测备考之工程问题中双人双工型

2022年-行测备考之工程问题中双人双工型

　　今天图图给各位考生梳理下工程问题比较复杂的一类题型—双人双工型。

　　双人双工题型一般是A、B两项工作，甲、乙两个人来做，每人做每项工作的效率不一样，求两项工作全部完成的最短时间。这类题型我们可以细分为下面两类：

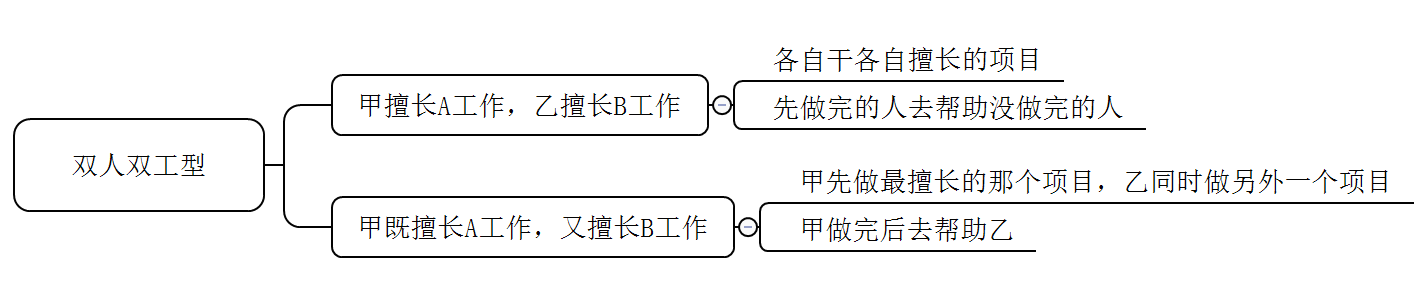
　　那么接下来我们用两道例题来阐述上面的这两种题型：

　　【例1】甲、乙两个工程队共同完成A和B两个项目。已知甲队单独完成A项目需13天，单独完成B项目需7天;乙队单独完成A项目需11天，单独完成B项目需9天。如果两队合作用最短的时间完成两个项目，则最后一天两队需要共同工作多长时间就可以完成任务?

　　A.1/12天B.1/9天

　　C.1/7天D.1/6天

　　本题考查工程问题，属于时间类中的双人双工型。用公式法解题。为满足合作时间最短，优先选择效率高的人员负责该项目。故甲负责B项目(甲7天优于乙9天)，乙负责A项目(乙11天优于甲13天)。当甲队第7天完成项目B后，为了确保用时最短，甲继续与乙队合作完成剩下的A。

　　赋值A的任务量为143(11和13的公倍数)，则甲的效率为143÷13=11，乙的效率为143÷11=13，设甲乙共同工作t天，可列方程：7×13+(11+13)t=143，解得t=，则最后一天共同工作天。因此，选择D选项。

	甲（时间）	乙（时间）	甲（效率）	乙（效率）
A项目(13×11=143)	13	11	11	13
B项目(7×9=63)	7	9	9	7

　　此题属于第一类题型，甲乙两人各自有擅长的项目，那么每人优先做自己擅长的项目，先做完的去帮助还没做完的人，这样安排用时最短。

　　【例2】梳理甲、乙两个案件的资料，张警官单独完成，分别需要2小时、8小时;王警官单独完成需要1小时、6小时。若两人合作完成，要的时间至少是：

　　A.3小时B.4小时

　　C.5小时D.6小时

　　本题考查工程问题，也属于时间类中的双人双工型。我们发现甲乙两个案件王警官用的时间都比张警官要少，所以此题属于双人双工型的第二类题型，一个人擅长两个项目。即王警官两个项目都擅长。

　　设甲案件的总量为2，乙案件的总量为24，则张警官的效率分别是1、3;王警官的效率分别是2、4，相对效率之比分别为1∶3和1∶2，可知王警官梳理甲案件，让张警官去梳理乙案件，王警官梳理甲案件需要1小时，此时乙案件还剩24-3=21的工作量，两人合作需要21÷(3+4)=3(小时)。一共需要1+3=4(小时)。因此，选择B选项。

　　经过上面两道题的阐述，相信各位考生也应该能分清楚这两类题型，并且遇到这两类题型也能快速的进行解答，在考场中能游刃有余，如鱼得水。