2022年备考干货：几何问题之平面几何

2022年备考干货：几何问题之平面几何

　　几何问题分为平面几何和立体几何。平面几何中常考的图形有三角形，正方形，长方形，圆形。立体几何中常考的有正方体，长方体，圆柱体，锥体，球体。接下来小编帮大家整理了2017年到2021年在云南联考中，几何问题的考试频次。

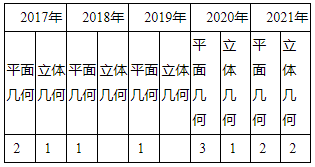
　　由表可知，几何问题在公考中每年都考，属于重点题型。那么接下来，我们就平面几何做一点小分享。

　　分享一：平面几何知识点分享

　　公式类：

　　三角形的面积S=底边×高/2;正三角形的面积S=(a是边长)

　　正方形的周长C=4a,正方形的面积S=a×a;

　　长方形的周长C=2×(a+b)，长方形的面积S=a×b;

　　圆形的周长C=2，圆形的面积S=

　　结论类：

　　周长一定的四边形，越靠近正方形，面积越大;

　　面积一定的四边形，越靠近正方形，周长越小。

　　分享二：真题讲解。

　　【例1】某商场为了促销，进行掷飞镖游戏。每位参与人员投掷一次，假设掷出的飞镖均扎在飞镖板上且位置完全随机，扎中中间阴影部分区域(含边线)即为中奖。该商场预设中奖概率约为60%，仅考虑中奖概率的前提下，以下四幅图形(图中的正三角形和正方形均与圆外切或内接)最适合作为飞镖板的是：

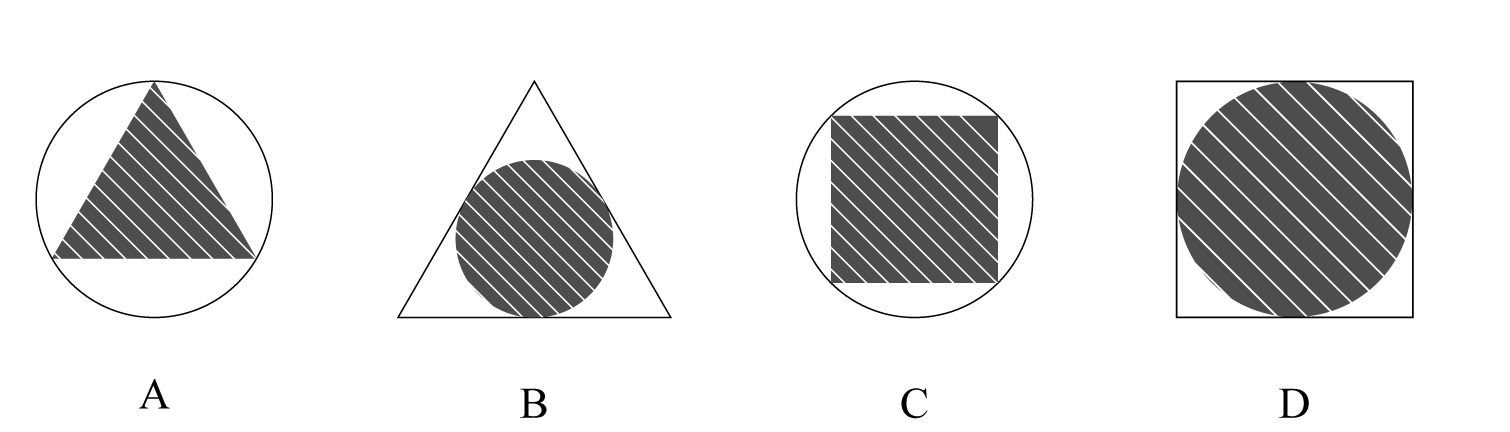
　　【答案】B

　　【解析】该商场预设中奖概率约为60%，则需要阴影部分的面积占整个图形的面积比值约是60%即可。A选项。赋值圆的半径是1，则圆的面积是，阴影部分当作正三角形计算，正三角形的边长是，则面积是，则比值是÷≈41%，不符合。B选项，赋值正三角形的边长是2，则正三角形的面积是，阴影部分圆的半径是，则圆的面积是，则比值是÷≈60.5%，符合。因此，选择B选项。

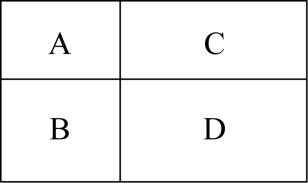
　　【例2】村民陶某承包一块长方形种植地，他将地分割成如图所示的4个小长方形，在A、B、C、D四块长方形土地上分别种植西瓜、花生、地瓜、水稻。其中长方形A、B、C的周长分别是20米、24米、28米，那么长方形D的最大面积是：

　　A.42平方米

　　B.49平方米

　　C.64平方米

　　D.81平方米

　　【答案】C

　　【解析】

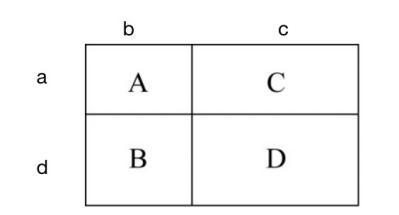
　　如图所示，假设A的长和宽分别是b和a,B的长和宽分别是b和d,C的长和宽分别是c和a,由题意知，列方程得a+b=10,b+d=12,a+c=14,可推出c+d=(b+d)+(a+c)-(a+b)=12+14-10=16,16是D的周长的一半，若需要D的面积最大，则把D构造成正方形，所以D的边长是16÷2=8，D的面积是64.因此，选择C选项。

　　要想学好平面几何，掌握公式是最基础的也是最重要的一步，其次要多加练习，多总结解几何题的思考逻辑。

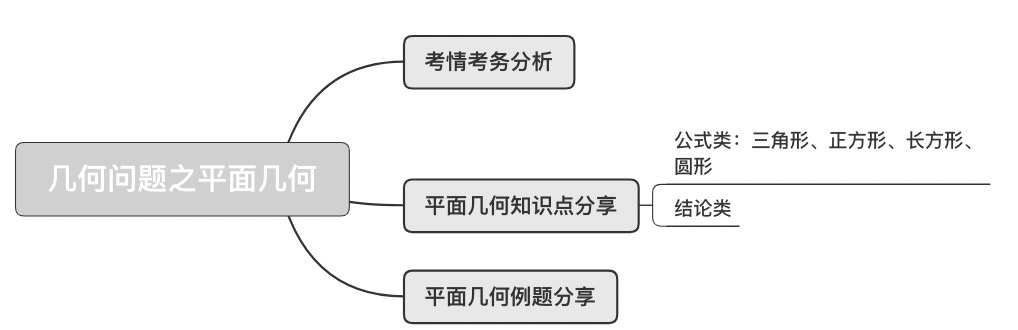
　　最后，把上述内容通过思维导图形式带大家进行回顾。