2021-10-15 10:36:39 国家公务员考试网 jl.huatu.com 文章来源:华图教育
2022年国考行测备考之双人双工程问题
在国联考中,工程问题是一个高频考点,常见的工程问题有给定时间型、效率制约型以及条件综合型这三类,除了常见的这三类题型,工程问题中还有一类效率统筹的问题,即双人双工程问题。那么,双人双工程问题题目有什么特点呢?该如何解题呢?
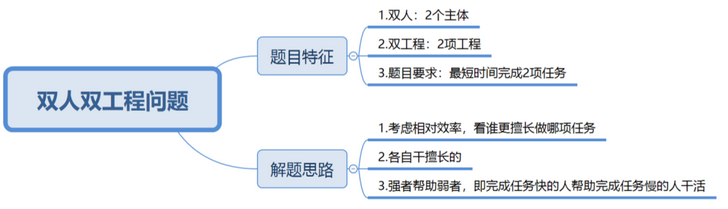
一、题目特征
1、一般给定甲、乙两个主体需要完成A、B两项任务;
2、要求最终用时最少。
二、解题方法
1.比较甲、乙做同一项任务的相对效率,即看谁更擅长做哪项务。
2.各自干擅长的;
3.强者帮助弱者,即完成任务快的人帮助完成任务慢的人干活。
三、真题讲解
【例1】甲、乙两家园林公司共同完成两个项目。已知甲公司单独完成项目Ⅰ需要3天,单独完成项目Ⅱ需要12天;乙公司单独完成项目Ⅰ需要5天,单独完成项目Ⅱ需要8天。并且甲公司在开工后的第2天,因故停工1天,那么,两家公司共同完成两个项目最少需要多少天?
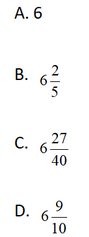
【答案】B
【解析】第一步,考虑相对相率:对于项目Ⅰ,甲3天优于乙5天,即甲的效率高于乙;对于项目Ⅱ,乙8天优于甲12天,乙的效率高于甲。为满足合作时间最短,优先选择效率高的人员负责该项目,故甲负责项目Ⅰ,乙负责项目Ⅱ。
第二步,各自干擅长的:甲公司在开工后的第2天因故停工1天,所以还需要2天就能完成项目Ⅰ;在这4天内乙负责项目Ⅱ,完成一半的任务量。
![]()
第三步,强者帮助弱者:项目Ⅰ已经由甲在4天完成,项目Ⅱ还剩余一半的任务量。要满足合作时间最短,则项目Ⅱ剩余一半的任务量由甲帮助乙,即甲乙合作完成。对于项目Ⅱ,乙单独完成需要8天,甲单独完成需要12天,赋值工作总量为24(12和8的公倍数),则甲完成项目Ⅱ的效率为,乙完成项目Ⅱ的效率为。剩余工作量为24-12=12,还需要天。故一共需要天。
因此,选择B选项。
【例2】甲、乙两条生产线生产A和B两种产品。其中甲生产线生产A、B产品的效率分别是乙生产线的2倍和3倍。现有2种产品各X件的生产任务,企业安排甲和乙生产线合作尽快完成任务,最终甲总共生产了1.5X件产品。问乙在单位时间内生产A的件数是生产B件数的多少倍?
![]()
【答案】C
【分析】例1是我们直接通过工作时间判定甲乙两公司在不同的项目各种优势,但是例2呢,我们会发现甲生产线在生产A、B两种产品都有绝对的优势,貌似乙生产线无明显优势。这种情况该怎么办呢?
【解析】第一步,考虑相对效率:甲在B产品的效率是乙生产线的3倍,明显高于A
产品的效率倍数。虽然甲做A、B两种产品均有优势,但是甲更加擅长做B产品。因此甲负责B产品,乙负责A产品。
第二步,各自干擅长的:甲先干B产品,由于效率高,B产品的X件完全由甲生产;此时乙干A产品未干完。
![]()
第三步,强者帮助弱者:甲干完B帮乙干A,由“共干1.5X件”可知A产品甲干了0.5X件;由于甲效率是乙的2倍可知在合作的时间里乙干了0.25X件。 那么乙在单干A产品的时候干了0.25X件。这个时间里甲以乙效率的三倍单干B干了X件,可知这个时间乙干B可以干件。由时间一致可知效率比为0.25X∶。
因此,选择C选项。
通过上面两个例题的分析,相信大家对双人双工程问题已经有了一定的了解,这类题目题目特征固定,解题思路通用。只要多加练习,一定能够攻克。
以上就是【2022年国考行测备考之双人双工程问题】的相关内容,如果要了解更多国考行测备考之双人双工程问题相关内容,欢迎关注吉林华图教育。

贴心微信客服
上一篇:2022年国考行测数量关系备考干货之翻过“分组问题”大山
下一篇:没有了