2021-08-19 08:59:58 国家公务员考试网 jl.huatu.com 文章来源:华图教育
2022年国考行测数量核心考点展望
纵观近几年的考试题目,我们不难发现有些类型的题目是必考的,比如工程问题,近五年出现了四道题目;再比如行程问题,近五年年年都有,甚至有些年份考两道题目。下面我们就分别看几个例题给大家讲解这两部分的知识点,我们一起来看例题:
【例1】某项工程如果由甲单独干6天完成总工程量的¼,剩余的由甲乙合作10天完成。如果此项工程由乙单独做,需要几天?
A.24
B.25
C.30
D.35
【答案】C
【解析】适用前提剖析:
整个题干中给出的量很容易求得效率比,是典型的效率类工程问题,用赋值法解题。
根据题干描述,可得甲单独6天干的量×3等于甲乙合作8天的量,如果设甲的效率为x,乙的效率为有,可得6x×3=10(x+y),整理可得8x=10y,即甲乙效率之比为5:4。
假设甲的效率=5,乙的效率=4,则可得总的工作量=6×5×4=120,故乙单独干需要天数t=120÷4=30天。因此,选择C选项。
【例2】一项工程,甲一人做完需30天,甲、乙合作完成需18天,乙、丙合作完成需15天,甲、乙、丙三人共同完成该工程需:( )
A.10天
B.12天
C.8天
D.9天
【答案】A
适用前提剖析:
整个题干中给出的都是完成时间,是典型的时间类工程问题,用赋值法解题。
【解析】赋工作总量为90(30、18、15的公倍数),根据题意可知,甲的效率为3,甲乙的效率为5,乙丙的效率为6,则乙的效率为2,丙的效率为4,故甲乙丙的效率和为2+3+4=9,所以三人共同完成需90÷9=10(天),因此,选择A选项。
【拓展】做题熟练的同学,其实这道题甲乙的效率这个条件可以不用,直接赋值总量30,甲的效率为1,乙丙的效率为2,然后计算即可。
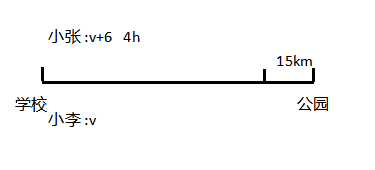
【例3】小张和小李两人上午8时同时从学校骑车到公园,小张每小时比小李快6千米。中午12时小张到达公园后立即返回学校,在距离公园15千米处遇到小李。求学校和公园相距多少公里?
A.50
B.60
C.70
D.80
【答案】B
适用前提剖析:
整个题干中给出了路程、速度和时间,根据描述可借助于行程图快速找到等量关系解题。
【解析】
设学校到公园的总距离为S,则相遇时两人所走的路程分别为S+15、S-15,所以两人的路程差为(S+15)-(S-15)=30。根据路程差=速度差×时间,可得30=6×时间,所以相遇时一共走了5小时。
小张上午8时出发,12时到公园,一共用了4个小时,可知返回来一共走了5-4=1小时,一共走了15公里,所以小张的速度为15公里/小时。S=15×4=60公里。因此选择B选项。
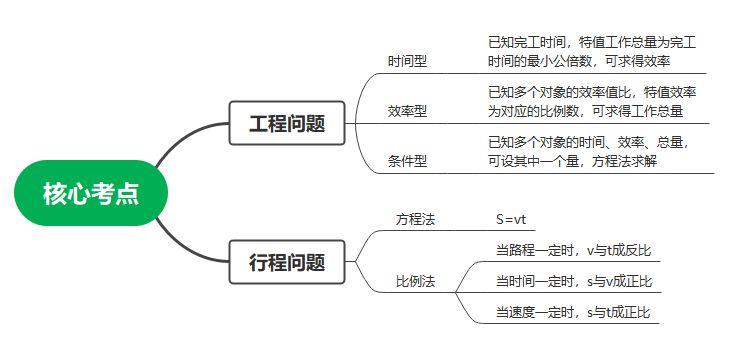
其实,工程问题和行程问题也没有太多知识点,大家着重掌握好以下几点,再加上一些题目的练习,相信在考场上就可以很快有思路算出答案。
最后,相信每个努力过的人都能攀登到自己理想的顶峰,领略最美的风景,俯瞰众山小,加油!
以上就是【2022年国考行测数量核心考点展望】的相关内容,如果要了解更多国考行测数量核心考点展望相关内容,欢迎关注吉林华图教育。

贴心微信客服