2021-07-01 09:33:11 吉林公务员考试网 jl.huatu.com 文章来源:净月华图
关注【吉林华图】公众号获取更多考试资讯  点击关注
点击关注
2022国考行测备考:几何问题中比例法的具体运用!
2022国考行测备考:几何问题中比例法的具体运用
近年来,公考中的几何问题无论是题量还是难度都有大幅提升,尤其是一些看起来较为复杂的几何题目,需要进行大量的计算,但考生在实际考试过程中往往没有充足的时间进行详细计算,所以在这里给大家介绍一种可以有效缩短解题步骤,降低计算难度的方法:比例法,希望通过这边文章,可以让大家体会到比例法的妙用。
在公考中,几何问题主要分四类:
1.镜像短距问题
2.同底等高问题
3.相似图形问题
4.勾股定理问题。
做题时候会涉及一些基本的面积、体积公式。在相似图形问题中,有几个重要的性质需要大家记住:
1.同一类的正多边形彼此相似,所有圆相互相似;
2.相似比=对应边的比,比如,两个圆的半径比、直径比或周长比就是二者相似比;
3.面积比=相似比的平方,体积比=相似比的立方。
除了相似比与比例有关面积、体积的求解往往也可以用比例法快速简化计算,所有形如A=B×C形式的公式,都能适当应用比例法而我们一般的面积、体积公式都基本符合这种形式比如:平行四边形面积=底×高;一般柱体体积=底面积×高;一般椎体体积=底面积×高÷3,对应上述公式,就有:体积与底面积、高分别成正比;高与底面积成反比
【例】(2020年安徽,)在屋内墙角处堆放稻谷(如图,谷堆为一个圆锥的四分之一),谷堆底部的弧长为6米,高为2米,经过一夜发现谷堆在重力作用下底部的弧长变为8米,若谷堆的谷量不变,那么此时谷堆的高为:
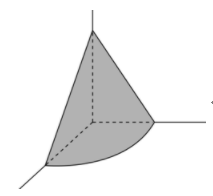
A.9/8米 B.8/9米 C.9/16米D.4/9米
【思路及解题过程】
看见“如图”就可以判定为几何问题问题,“若谷堆的谷量不变,那么此时谷堆的高为”谷量不变,就是指体积不变问高变为多少,而图给出的是一个圆锥的1/4,那么,马上可以想到圆锥体积公式:体积=底面积×高÷3,如果按公式先算出体积,再算出后来的底面积继而相除得到新的高,这思路自然是可以行得通的。但是这样求解本题,不可避免的就会加大计算量,体积公式的形式以及“体积不变”还是比较容易想到比例法,那么,就可以避免计算体积甚至底面积都不需要计算,显然比常规思路快很多。
再看图形,虽然前后两个谷堆不是相似圆锥,但是出现了“圆”的概念相关的可以想到“所有的圆都相似”而谷堆底面,虽然不是圆,但都是1/4圆,扇形自然也是相似的。那么前后底面积的比就为他们相似比的平方,而相似比就是对应边的比例。对照题干,关于底面给出的都是弧长,也就是对应的边,所以,谷堆前后相似比为前:后=6:8=3:4,则谷堆前后面积比为前:后=(3×3):(4×4)=9:16。因为谷堆体积不变,所以高和底面积成反比,所以,谷堆高的比为前:后=16:9=(16×8):(9÷8)=2:(9/8),即原来高为2米,则,后来高为9/8米,故本题选A。
这一题主要是给大家展示了相似比在具体题目中的识别和应用,以及比例法的使用。这题如果按部就班的进行计算,先通过弧长求前后底面扇形半径、面积,光推导过程估计都要花很长时间,考场时间宝贵,所以一定要学会综合应用所学知识。上述讲解看起来繁琐,但事实上前面文字部分不过是在大脑中就可以完成的思维过程,实际做题的过程中,只要可以熟练运用比例法,相信大家一定可以在很短的时间内将这类题快速准确的求解出来。
以上就是【2022国考行测备考:几何问题中比例法的具体运用!】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了