2022国考公务员行测容斥原理在资料分析中的应用

2022国考公务员行测容斥原理在资料分析中的应用

　　2021年国考笔试已经结束，今年考试的资料分析部分出现了一道运用数量关系容斥原理思维解决的题目，这在国考中是比较少见的。资料分析中的容斥问题相对比较简单，侧重于容斥基本公式的考查，常考查二集合容斥相关问题。

　　对于二集合容斥，基本公式为：总数-两者都不满足的个数=A+B-AB都满足的个数。

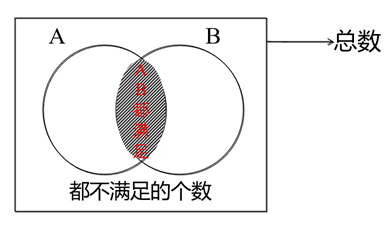
　　接下来，我们一起看一下二集合容斥在资料中的具体考查方向：

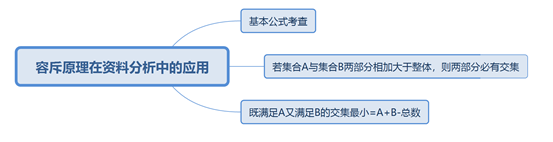
　　1、基本公式考查

　　【例1】截至2019年末，全国已有残疾人康复机构9775个，比2018年增长739个。2019年，1043.0万残疾儿童及持证残疾人得到基本康复服务，其中包括0—6岁残疾儿童18.1万人。

　　如提供视力残疾康复服务的残疾人康复机构中，同时提供听力言语残疾康复服务的机构比不提供该服务的机构多20%，则2019年末全国有多少家残疾人康复机构不提供以上两种康复服务中的任意一种?

　　A.不到7300家

　　B.7300—7600家之间

　　C.7600—7900家之间

　　D.超过7900家

　　【答案】B

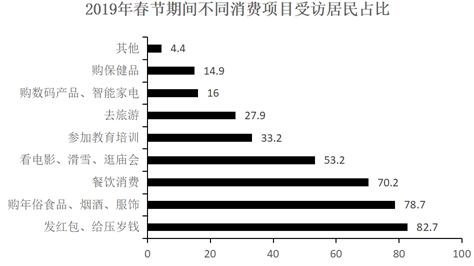
　　【例2】2019年春节期间有“餐饮消费”的受访居民中，一定有人：

　　A.参加教育培训

　　B.去旅游

　　C.购保健产品

　　D.购数码产品、智能家电

　　【答案】A

　　【解析】要想“餐饮消费”受访居民中一定有人去参加另一个消费项目，则使二者占比加和>100%即可。“餐饮消费”受访居民占比70.2%，两个项目占比满足大于100%的只有“参加教育培训”(33.2%)。

　　因此，选择A选项。

　　在集合A中，集合B最少，即既满足A又满足B的交集最少

　　方法：既满足A又满足B的交集最少=A+B-总数。

　　根据二集合容斥基本公式，总数-两者都不满足的个数=A+B-AB都满足的个数，AB都满足的个数=A+B-总数+两者都不满足的个数，要让AB都满足的个数最少，可让两者都不满足的个数为0。

　　如班级有42名同学，喜欢小说的有25人，喜欢诗歌的有30人，问既喜欢读小说又喜欢读诗歌的同学至少又多少人?根据基本公式，42-都不喜欢=25+30-都喜欢，都喜欢=13+都不喜欢，都不喜欢的同学最少为0时，都喜欢最少为13名同学。

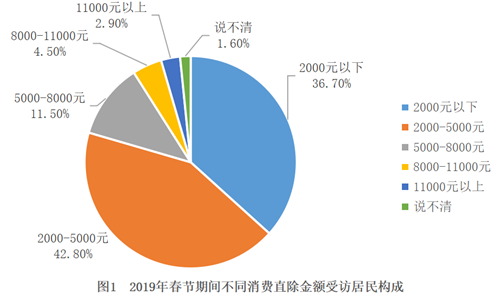
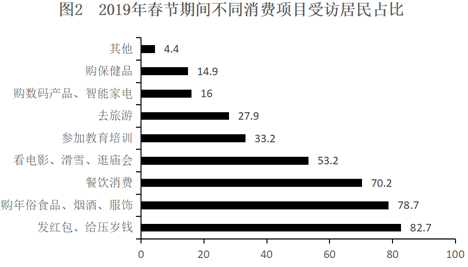
　　【例3】2019年春节期间消费支出在2000元以下的受访居民，“发红包，给压岁钱”的至少占：

　　A.79.4%

　　B.61%

　　C.54.8%

　　D.52.9%

　　【答案】D

　　【解析】根据部分量=整体量×比重，整体量一致时，可以用占比代替真实的人数，“2000元以下受访居民”与“发红包，给压岁钱”的交集最小为36.7%+82.7%-100%=19.4%，当二者交集最小时，2000元以下受访居民中发红包，给压岁钱的占比也最小，为19.4%÷36.7%≈52.9%。

　　因此，选择D选项。

　　一般来说，容斥问题在资料分析中的考查多涉及调查或统计材料，题目本身不难，多加练习，识别题型，是可以快速掌握的。

以上就是【2022国考公务员行测容斥原理在资料分析中的应用】的相关内容，如果要了解更多公务员行测,公务员考试相关内容，欢迎关注吉林华图教育。