2022国考行测备考数量关系：比例法在行程问题中的应用

2022国考行测备考数量关系：比例法在行程问题中的应用

　　行程问题在历年公职考试当中，一直是考生公认的难题模块，主要是由于行程问题考查的是考生对物体运动过程的理解，通常会把运动过程描述的非常复杂，如果不能抓住其中物体运动的一些比例关系，运用常规的解题思路，会浪费大量的时间，因此在考试时间紧迫的情况下，需要找到更快捷的一种解题方法。在此介绍比例法来帮助考生快速解决一些行程问题。

　　根据行程问题的基本公式可知：

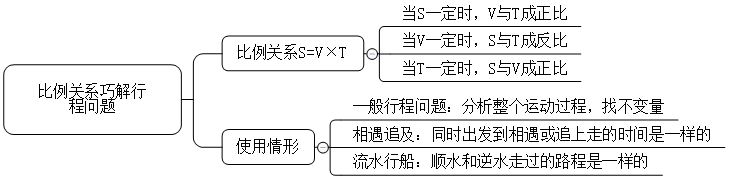
　　当s一定时，v与t成正比;

　　当v一定时，s与t成反比;

　　当t一定时，s与v成正比。

　　以上就是比例法的原理，原理非常简单，当题目中告诉我们某个量一定、并且给出其他量的比例关系时，就要想到用比例法。比例法在我们基本行程问题、相遇追及问题、流水行船问题中都有广泛应用。下面通过具体例子来说明比例法在行程问题中的应用。

　　比例法在基本行程问题中的应用

　　【例1】小王步行的速度比跑步慢50%，跑步的速度比骑车慢50%。如果他骑车从A城去B城，再步行返回A城共需要2小时。问小王跑步从A城去B城需要多少分钟?( )

　　A. 45 B. 48

　　C. 56 D. 60

　　解析：【B】题目给出了速度的比例关系，且从A城到B城，再从B城返回A城走的路程一样，可以考虑比例法。假设小王步行的速度为1，则跑步的速度为2，骑车的速度为4，即小王骑车的速度和步行的速度之比为1:4;小王骑车从A城去B城，再步行返回B城，骑车和步行所走的路程是一定的，因此所用的时间之比为4:1，即小王骑车从A城到B城所用的时间为15×120=24分钟。而小王跑步的速度是骑车的一半，所以小王跑步从A城去B城需要48分钟。

　　比例法在相遇追及问题中的应用

　　【例2】一辆客车与一辆货车从东、西两个车站同时出发匀速相向而行，客车和货车的行驶速度之比为4:3。两车相遇后，客车的行驶速度减少10%，货车的行驶速度增加20%，当客车到达西车站时，货车距离东车站还有17公里。东、西两个车站的距离是( )公里。

　　A. 59.5 B. 77

　　C. 119 D. 154

　　解析：【C】两车同时出发相向而行，两车相遇后，经过的时间是一定的，因此所走的路程和速度成正比为4:3，全程共7份，根据题意可知，两车相遇后速度变为了一样。当客车到达西站时，货车距离车站还有17公里，即全程共17×7=119公里。

　　比例法在流水行船问题中的应用

　　【例3】A和B两个码头分别位于一条河的上下游，甲船从A码头到B码头需要4天，从B码头返回A码头需要6天;乙船在静水中速度是甲船的一半。乙船从B码头到A码头需要( )天。

　　A. 667 B. 767

　　C. 12 D. 16

　　解析：【D】甲船从A到B，再从B到A所走的路程是一定的，因此甲船顺水的速度和逆水的速度之比为6:4.设甲船顺水的速度为6，则逆水的速度为4，根据流水行船的公式可知，甲船的速度为5，水的速度为1。则AB的距离为24，乙的速度为2.5，乙从B到A是逆水的过程，因此需要24/(2.5-1)=16。

　　通过对上述几个例题的分析，大家会发现在行程问题中巧用比例关系会大大提高解题速度。更多解题技巧，请大家关注华图微信公众号。

　　解更多备考知识，可以关注卫星华图，微信号：wxht81864889

以上就是【2022国考行测备考数量关系：比例法在行程问题中的应用】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。