事业单位：最不利构造_靖宇华图

事业单位：最不利构造_靖宇华图

　　事业单位考试中，数量关系考察最值问题的题目基本每年都会涉及，这也符合事业单位考察统筹能力的考情要求，最值问题包括：最不利构造、数列构造和多集合反向构造，我们今天就单独讨论一下其中的最不利构造。

　　要熟练掌握最不利构造问题，我们首先要解决的问题是这种题型的识别特征是什么?解题思路是什么?需要注意什么等等。下面就进行一一阐述。

　　题型特征：“至少…保证…”。

　　解题思路：所有不利情况+1。

　　接下来，我们就看一下具体的例题。

　　【例1】有软件设计专业学生90人，市场营销专业学生80人，财务管理专业学生20人及人力资源管理专业学生16人参加求职招聘会，问至少有多少人找到工作就一定保证有30名找到工作的人专业相同?

　　A.59B.75

　　C.79D.95

　　【解析】第一步，本题考查最值问题，属于最不利构造。

　　第二步，最不利构造类题目的答案为“所有不利情况+1”。由于30名找到工作的人专业相同，确定所有不利情况为各专业的人尽量多且小于30人，即软件设计29人，市场营销29人，财务管理20人，人力资源16人。

　　第三步，故至少需要29+29+20+16+1=95(人)找到工作，就一定保证有30名找到工作的人专业相同。

　　因此，选择D选项。

　　【例2】(2015.10.31联考A类-43)某公司有38名男员工，27名女员工。现要参加集团组织的羽毛球比赛，如采取自由报名的形式，至少有多少名员工报名才能保证一定能从报名者中选出男女选手各8名参赛?

　　A. 65B. 46

　　C. 35 D. 16

　　【答案】B

　　【解析】第一步，本题考查最值问题，属于最不利构造，用公式法解题。

　　第二步，根据“至少……保证……”可知本题为最不利构造问题，可根据固定步骤：答案=最不利值+1求解。本题的最不利情况为：男员工离“8名参赛”差1人或女员工离“8名参赛”差1人。分析可知，由于男选手人数较多，则当38名男选手全部选出且女选手只选出7名时为最不利的情况，即最不利值=38+7=45;

　　第三步，接下来只需再选一人，即可满足保证一定能从报名者中选出男女选手各8名参赛。答案=45+1=46。

　　因此，选择B选项。

　　【例3】(2018.5.26联考-41)某公司市场部有五个业务小组，分别有6人、7人、8人、11人、14人，一次拓展活动中计划设置抽奖环节，规则为每人最多只能抽到1份奖品。为保证每个小组都至少有两人抽到奖品，最少应准备多少份奖品?

　　A. 10B. 23

　　C. 34D. 42

　　【答案】D

　　【解析】第一步，本题考查最值问题，属于最不利构造。

　　第二步，出现“保证”、“至少”，考虑最不利情形，五个小组人数分别为6人、7人、8人、11人、14人，最不利情形为除人数最少的组以外其他四个组全都抽到奖，而人数最少的小组只有1人抽到奖，此时中奖人数为14+11+8+7+1=41，不满足每个小组都至少有两人抽到奖品，但只要再有1人中奖就能保证满足题目要求，即最少应准备42份奖品。

　　因此，选择D选项。

　　【例4】某单位组织党员参加党史、党风廉政建设、科学发展观和业务能力四项培训，要求每名党员参加且只参加其中的两项。无论如何安排，都有至少5名党员参加的培训完全相同。问该单位至少有多少名党员?

　　A. 17B. 21

　　C. 25D. 29

　　【答案】C

　　【解析】第一步，标记量化关系“无论如何”、“至少”、“至少”。

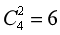
　　第二步，根据“无论如何”、“至少”可知，本题为最不利构造问题，答案为“所有不利情况数+1”。考虑最不利情况为每种方案都有4名党员参加，而共有种方案(四项培训中选择两项参加)，故所有不利情况数为：6*4=24。

　　第三步，该单位“至少”有24+1=25名党员。

　　因此，选择C选项。

　　综上所述，关于最不利构造问题，我们只要会识别题型(只要出现“至少…保证…”)，按照解题方法(所有不利情况+1)去做就没问题，大家学会了吗?

　　更多资料及讯息请联系靖宇华图：0439-7238886

以上就是【事业单位：最不利构造_靖宇华图】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。