2020年吉林省考备考： 几何中的极值问题

2020年吉林省考备考： 几何中的极值问题

　　几何问题在公考中出现的频率相当高，一方面在考题中经常会出现问最多、最大等极值问题，另一方面，在几何问题中用极值的思维解题会大大提高解题效率，今天我们就来看一下几何题中的极值如何运用。

　　几何中的极值问题通常有三种类型：

　　(1)利用几何特性求极值

　　(2)利用图形分析求极值

　　(3)利用极端假设求极值

　　下面我们分别了解一下：

　　一、利用几何特性求极值

　　例题详解

　　【例1】相同表面积的四面体、六面体、正十二面体及正二十面体，其中体积最大的是?( )

　　A. 四面体B. 六面体

　　C. 正十二面体D. 正二十面体

　　【答案】D

　　【解析】根据几何的最值理论：立体图形中，若表面积一定，越接近于球，体积越大。四个选项中，正二十面体最接近球形，因此体积最大，答案选D

　　总结：常用的几何最值理论有

　　平面图形中，若周长一定，越接近于圆，面积越大;

　　平面图形中，若面积一定，越接近于圆，周长越小;

　　立体图形中，若表面积一定，越接近于球，体积越大;

　　立体图形中，若体积一定，越接近于球，表面积越小。

　　二、利用图形分析求极值

　　例题详解

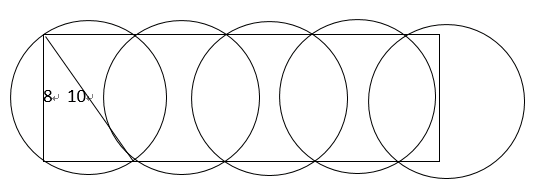
　　【例2】现要在一块长25公里、宽8公里的长方形区域内设置哨塔，每个哨塔的监视半径为5公里，如果要求整个区域内的每个角落都能被监视到，则至少需要设置多少个哨塔? ( )

　　A. 4B. 5

　　C. 6D. 7

　　【答案】B

　　【解析】用哨塔覆盖长方形区域，即用圆覆盖长方形，想要圆最少，则每个圆形覆盖的长方形面积应该尽可能大，且圆和圆之间的衔接面积尽量小，所以覆盖方式如下图，圆的直径为10，长方形宽8，根据勾股定理每个圆覆盖的长方形的长度为6，25÷6=4…1，所以需要五个圆进行覆盖，即五个哨塔，答案选择B。

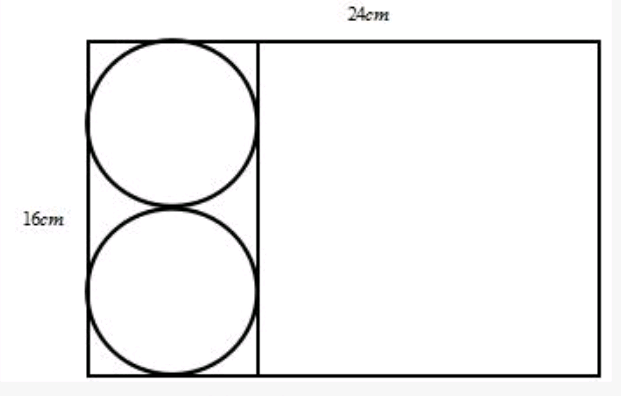
　　【例3】(2018年国考)将一块长24厘米，宽16厘米的木板分割成一个正方形和两个相同的圆形，其余部分弃去不用。在弃去不用的部分面积最小的情况下，圆的半径为多少厘米? ( )

　　A. 2√2B. 4

　　C. 3√2D. 8

　　【答案】B

　　【解析】将木板切割，丢弃面积最小的情况下，因为正方形没有丢弃的部分，所以正方形的面积要尽量大，正方形最大能切割成边长16cm，即和整体长方形的宽一样。所以切割完正方形之后，剩下的面积为长为24-16=8cm，宽为16cm的新长方形。此时切割圆，圆的面积尽量大，则两个圆相切且与长方体的边相切，切割方式如图。此时的圆的半径为8÷2=4cm，答案选择B。

　　总结：几何计算过程中求极值，需要分析几何图形特征，同时需要空间想象力。一般计算极值时，考虑让图形处于极值状态，例如：相切、相等、最大等情况。

　　三、利用极端假设求极值

　　例题详解

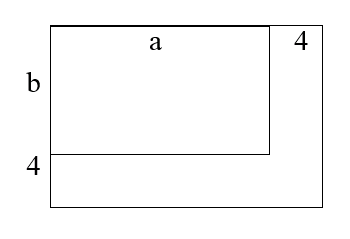
　　【例4】(2017年联考)某单位准备扩建一矩形花圃，若将矩形花圃的长和宽各增加4米，则新矩形花圃的面积比原来的面积增加了40平方米。那么，原矩形花圃的周长是多少? ( )

　　A. 12B. 24

　　C. 32D. 40

　　【答案】A

　　【解析】利用通常解法，如下图所示，设矩形花圃的长为a，宽为b，将增加面积看做两个矩形，则增加的面积表示为：得到，矩形周长为

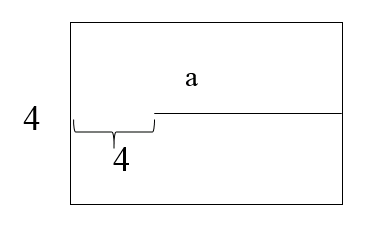
　　如果利用极端假设，因为题目中只给了增加的宽度和增加的面积，没有给原矩形边长的限定，所以假设原矩形的长为a，宽为0，则原矩形变为一条直线，增加部分即变为一个矩形，如下图所示：

　　则增加部分的面积表示为：，解得a=6，则原矩形周长为2a=12

　　【例5】有一周长为100米的长方形花园，在花园外围沿花园建一条等宽的环路，路的面积为600平方米，则路的宽度为( )米?

　　A. 3或4B. 5

　　C. 8D. 10或15

　　【答案】B

　　【解析】普通解法将长方形的长和宽设为a和b，增加的环路宽为d，如下图所示，则原周长为：，增加的面积为，利用方程组解得d=5，这种方法求解比较麻烦;

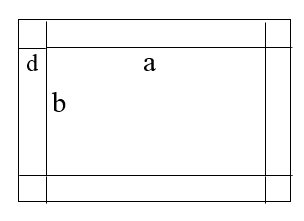
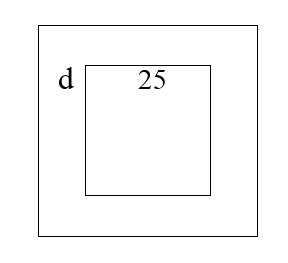
　　但若将矩形假设为边长相等的正方形，则如下图所示，此时正方形边长为25，环形路宽d

　　环形路的面积为：，解得d=5。

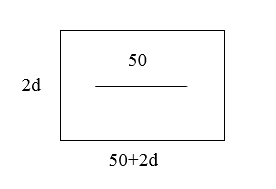
　　这种方法计算过程变得简单一点，但如果继续进行极端假设，将长方形假设为宽是0的两条重合线段，此时线段的长为50，则环形路的宽为2d，长为50+2d，如下图所示

　　则环形路的面积为，解得d=5，也可以用带入排除法计算，计算量变得更小。

　　所以题中如果没有对图形的边长进行限定，利用极端假设，将图形变得简单，甚至变成线段。

　　以上就是几何问题中常见的极值问题，既需要我们对几何特性有所了解，也需要我们有空间想象力，对图形进行合理设定。